 Чтобы осуществить переход из одного пункта земного шара в другой, судоводитель должен заблаговременно выбрать наивыгоднейший путь, а во время перехода вести учет движения своего судна.
Чтобы осуществить переход из одного пункта земного шара в другой, судоводитель должен заблаговременно выбрать наивыгоднейший путь, а во время перехода вести учет движения своего судна.
Для этого он должен иметь подробное изображение поверхности Земли, включающее в себя такие сведения, как очертание берегов, данные о глубинах моря, фарватерах, навигационных опасностях, береговых и плавучих средствах ограждения опасностей и т. д.
Применение глобуса для такого подробного изображения района плавания судна невозможно. Поэтому для судовождения применяют изображение отдельных, сравнительно небольших участков поверхности Земли, выполненное на плоскости.
Уменьшенное изображение на плоскости части или всей земной поверхности называется картой.
На практике применяют различные способы изображения сферической поверхности Земли на плоскости. Все они сводятся к построению по определенному математическому закону сетки прямых или кривых линий, изображающих параллели и меридианы. Совокупность этих линий на карте носит название картографической сетки, а способ, примененный для их изображения, называют картографической проекцией. Имея на плоскости систему координатных линий, можно нанести на нее изображение различных элементов земной поверхности по их координатам.
В любом случае изобразить сферическую поверхность на плоскости невозможно без разрывов и складок. Поэтому все картографические проекции имеют те или иные искажения, которые следует учитывать при пользовании картой.
Картографическая проекция - это способ отображения сферической поверхности земного шара на плоскости. Связанное с этим преобразование изображения неизбежно приводит к искажениям. Тем не менее некоторые характеристики картографической сетки, нанесенной на поверхность глобуса, могут быть сохранены и на карте за счет других характеристик, которые подвергнутся искажению. На глобусе все параллели и меридианы пересекаются под прямыми углами.
Проекция, в которой сохраняется это свойство, называется конформной, или равноугольной. В этом случае сохраняется форма площадных объектов, но относительные размеры меняются от места к месту. При другом способе преобразования можно сохранить правильное соотношение площадей (соответствующее исходной поверхности земного шара), но в этих случаях наблюдается искажение углов пересечения меридианов и параллелей; прямые углы сохраняются лишь в ограниченной зоне.
Проекции, в которых сохраняется правильное соотношение площадей отдельных ячеек градусной сетки, называются равновеликими; для них характерно большее или меньшее нарушение подобия фигур.
Правильная передача конфигурации объектов, как и правильная передача площадей, имеют большое значение, особенно если речь идет о мелкомасштабных обзорных картах.
Однако обе эти характеристики не могут быть совмещены на одной и той же карте: не существует проекции, которая была бы одновременно равноугольной и равновеликой. Кроме того, очень важен правильный показ расстояний и направлений. До некоторой степени этого удается достичь при использовании определенных проекций.
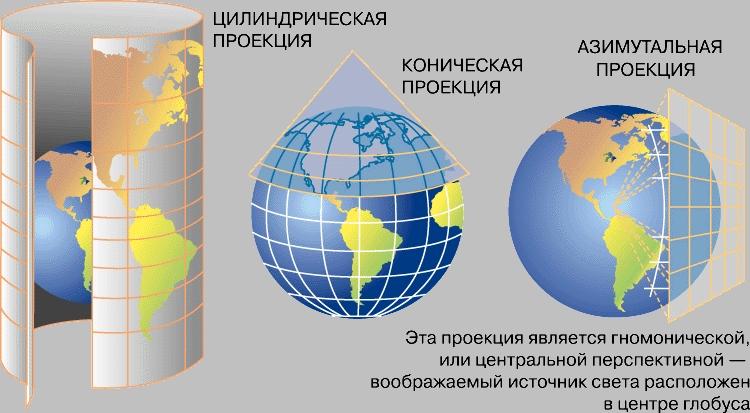
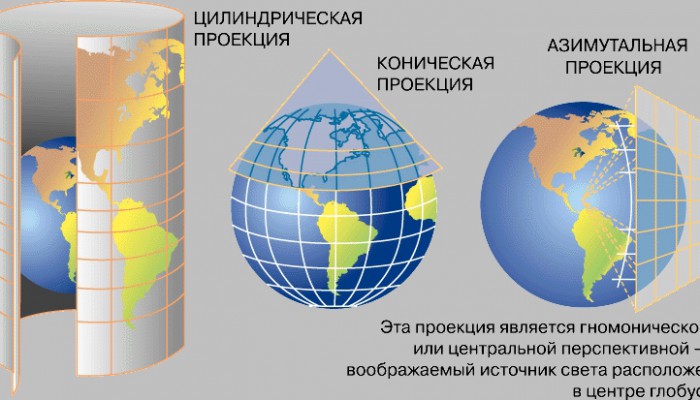
Картографические проекции можно классифицировать по виду вспомогательной геометрической поверхности, которая может быть использована при ее построении. Возьмем прозрачный глобус с нанесенными на его поверхность линиями меридианов и параллелей и точечный источник света.
Мы можем заключить глобус (с источником света, расположенным в центре шара) в цилиндр. При этом градусная сетка спроектируется на поверхность цилиндра, который затем может быть развернут на плоскости.
Цилиндр может быть касательным и соприкасаться с глобусом только по одной линии (например, экватора), а может быть секущим. В последнем случае поверхности шара и цилиндра будут совпадать по двум линиям (например, по 45° с.ш. и по 45° ю.ш.), и только по этим линиям в данной проекции сохраняется правильный масштаб.
При изменении положения источника света по отношению к поверхности шара могут быть получены различные проекции картографической сетки на поверхность цилиндра или другой геометрической фигуры.
ПОНЯТИЕ О ЛОКСОДРОМИИ И ОРТОДРОМИИ. ТРЕБОВАНИЯ, ПРЕДЪЯВЛЯЕМЫЕ К МОРСКОЙ КАРТЕ
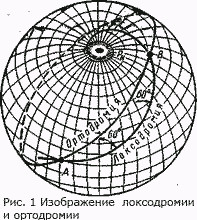
Если судно, совершая плавание между двумя пунктами, идет постоянным курсом, то оно пересекает все меридианы под одним и тем же углом. Линия, пересекающая все меридианы под постоянным углом, называется локсодромией (греч. «кривой бег»).
На поверхности земного шара локсодромия в общем случае изображается в виде спирали, стремящейся к полюсу, которого она не достигает (рис. 1). На курсах 0 и 180° локсодромия совпадает с меридианом, а на курсах 90 и 270° - с параллелью.
Плавание по локсодромии, т. е. постоянным курсом, удобно, так как не требует проведения каких-либо расчетов, связанных с частой переменой курсов. Однако локсодромия не является кратчайшим расстоянием между двумя точками A и В. Кратчайшим расстоянием между выбранными точками на земном шаре является меньшая из дуг большого круга, проходящего через эти точки (см. рис. 1). Эта дуга называется ортодромией (греч. «прямой бег»). Ортодромия пересекает все меридианы под разными углами. В частных случаях, при плавании по экватору или курсами 0 или 180°, она может совпадать с экватором или меридианами, которые одновременно являются локсодромиями.
Изображение локсодромии и ортодромии
При небольших переходах разность в длине мeжду локсодромией и ортодромией незначительна. Из-за удобства плавания по локсодромии на практике таким увеличением длины пути пренебрегают и совершают переходы постоянными курсами. Только в случае длительных океанских переходов плавание совершают по дуге большого круга.
Для судовождения требуется особая картографическая проекция, которая должна быть удобной для ведения графического счисления пути судна и определения его места.
Поэтому к морским картам предъявляются следующие основные требования:
- линия пути судна, идущего постоянным курсом, т. е. по локсодромии, должна изображаться на карте прямой линией, что обеспечит удобство прокладки курсов судна;
- углы и направления на местности должны быть равны соответствующим углам и направлениям на морской карте, т. е. карта должна быть равноугольной (конформной). Это позволит определять место судна в море по пеленгам и углам, измеренным между береговыми ориентирами, а также опознавать берег по его изображению на карте.
Проекцию, удовлетворяющую этим требованиям, создал в 1569 г. голландский картограф Герард Кремер, известный под именем Меркатора. Предложенная им проекция получила название меркаторской.
По способу построения она относится к нормальным (прямым) цилиндрическим проекциям; а по характеру искажений - к равноугольным, или конформным.
ЭЛЕМЕНТАРНАЯ ТЕОРИЯ МЕРКАТОРСКОЙ ПРОЕКЦИИ. ПОНЯТИЕ О ПЛАНАХ
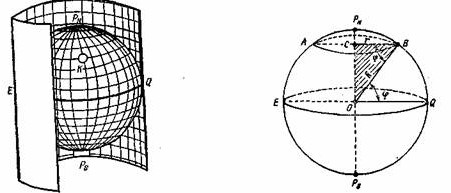
Картографическая сетка меркаторской проекции строится следующим образом. Условный глобус заключается в цилиндр, касательный глобусу по экватору (рис. 2).
Меридианы, нанесенные на глобус, распрямляются до тех пор, пока они не коснутся внутренней поверхности цилиндра. При этом меридианы образуют на поверхности цилиндра ряд прямых линий, параллельных между собой. Расстояние между этими .линиями равно расстояниям между меридианами на экваторе глобуса.
При распрямлении меридианов параллели растягиваются и становятся равными по длине экватору. На внутренней поверхности цилиндра они обра зуют ряд окружностей. Удлинение параллелей будет тем значительнее, чем ближе они к полюсу.
Картографическая сетка меркаторской проекции
Найдем математическую закономерность, которая определяет характер растяжения каждой параллели. Обозначим (рис. 3) радиус параллели АВ, лежащей в широте φ, через r, а радиус Земли — через R. В прямоугольном треугольнике ВОС<СВО = <BOQ= φ. Из этого треугольника получаем:
![]()
![]()
Умножив левую и правую части равенства на 2π, получим в левой части длину экватора, а в правой — длину параллели, умноженную на секанс широты данной параллели,
![]()
Из выражения (*) можно сделать заключение, что любая параллель, удлиняясь до окружности экватора, растягивается пропорционально секансу широты.
Разрежем цилиндр по образующей и развернем его на плоскость. Полученная картографическая сетка удовлетворяет первому требованию к морской карте: так как все меридианы параллельны, то локсодромия изобразится на ней прямой линией.
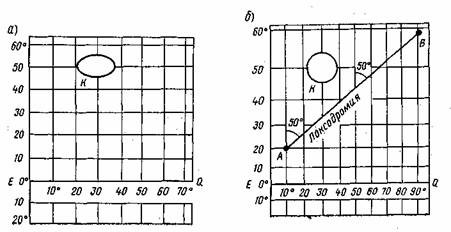
Однако проекция не является равноугольной, поскольку участки земной поверхности при проектировании будут вытягиваться на ней вдоль параллелей пропорционально секансу φ и, следовательно, не будет сохраняться подобие фигур на местности и на карте, Так, небольшой остров К имеющий круглую форму,изобразится в виде эллипса, вытянутого в широтном направлении (см. рис. 4, а).
Чтобы сделать проекцию равноугольной, необходимо теперь меридианы в каждой точке растянуть так же, как в этой точке растянулась параллель, т. е. пропорционально секансу широты точки.
После этого масштаб на каждом небольшом участке карты станет одинаковым как по параллели, так и по меридиану (рис. 4, б).Изображение круглого острова на картографической сетке сохранит свою круглую форму, т. е. проекция будет обладать свойством равноугольности.
Построенная таким методом картографическая проекция, удовлетворяющая обоим требованиям к морской карте, носит название меркаторской.
Масштаб полученной проекции меняется при перемене широты, оставаясь постоянным по направлению параллелей. Поэтому при составлении меркаторской карты главный масштаб указывается по одной из параллелей.
За главную параллель может приниматься средняя параллель участка земной поверхности, охватываемого данной картой. Однако при построении карт сравнительно мелкого масштаба за главную, как правило, принимается стандартная параллель данного моря или широтного пояса, даже если она не проходит через карту.
Рис. 4. Построение меркаторской проекции: a - сетка из меридианов и параллелей; б - меркаторска я проекция
Чтобы было удобно измерять расстояния, а также разности широт, боковые рамки меркаторской карты разбивают на участки в 1/, т. е. на морские мили. Так как при построении карты меридианы вытягивались не равномерно, а пропорционально секансу широты в каждой точке, то морские мили будут изображаться разными по длине участками, увеличивающимися по мере удаления от экватора.
Изображение 1 морской мили на меркаторской карте в данной широте называется меркаторскрй милей.
На экваторе, т. е. в широте 0°, меркаторская миля равна 1 экваториальной миле, в широте 60° - 2 экваториальным Милям (sec 60°= 2), а в широте 80° - 5,8 экваториальным милям (sec 80° = 5,8). При изменении расстояния в какой-либо широте следует пользоваться меркаторскими милями, взятыми с боковой рамки карты в той же широте.
Для изображения небольших участков - акваторий портов, гаваней, рейдов и т. д. применяются планы.
Планом называется плоское изображение небольших участков земной поверхности, кривизной которых можно пренебречь. По этой причине план не имеет искажений, сохраняя подобие фигур и площадей. Его составляют путем непосредственной съемки местности с заданным уменьшением размеров объектов. Масштаб плана сохраняется постоянным для всех его точек.
Масштаб карты определяется как отношение длины прямой между двумя точками на карте к действительному горизонтальному расстоянию между этими же точками на местности. Различают два вида масштаба: числовой (численный) и линейный.
Числовой масштаб - дробь, числитель которой единица, а знаменатель - число, показывающее, скольким единицам длины на местности равна одна единица на карте.
Линейный масштаб может быть выражен числовым соответствием единиц длины (например, "3 мили в 1 см") или графически. На морских картах линейный масштаб наносят на вертикальные рамки карты.
При развертывании сфероидической поверхности Земли на плоскость возникают искажения, вследствие чего степень уменьшения изображения в разных частях карты различна.
Другими словами, масштаб карты меняется при переходе от точки к точке. Масштаб, присущий данной точке карты, называется частным. В заголовках карт указывается числовой масштаб, близкий к среднему значению частных масштабов карт данного моря или района. Такой масштаб называется главным.
Минута широты, т.е. линейная величина 1 минуты дуги меридиана, представляет собой морскую милю. Морские мили будут изображаться на меркаторской карте разными по длине участками меридианов, увеличивающимися по мере удаления от экватора.
Графическое изображение 1-й морской мили на меркаторской карте на данной широте называется меркаторской милей. Измерять расстояние на карте следует меркаторскими милями на соответствующей им широте.