Небесной сферой называют вспомогательную сферу, построенную произвольным радиусом, на которую спроектированы светила. За центр сферы обычно принимают точку О, соответствующую глазу наблюдателя.
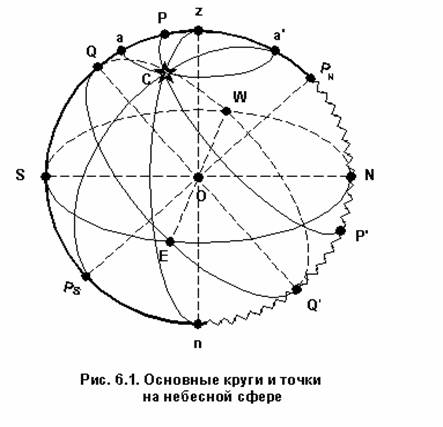
На рис. изображена небесная сфера для наблюдателя, расположенного в некоторой точке земной поверхности в северной широте f.
Отвесная линия, проходящая через центр и совпадающая с направлением силы тяжести, пересекает небесную сферу в точках зенита “г” и надира “п”. Плоскость, перпендикулярная отвесной линии и проходящая через центр сферы, называется плоскостью истинного горизонта, которая при пересечении с небесной сферой образует большой круг NESW.
Линия PnPs, параллельная оси вращения Земли, называется осью мира, а точки ее пересечения с небесной сферой полюсами мира: северным PN и южным Ps. Полюс, расположенный в надгоризонтной части сферы, называется повышенным, а в подгоризонтной - пониженным. Наименование повышенного полюса всегда одноименно с наименованием широты наблюдателя. Большой круг QEQ'W, плоскость которого перпендикулярна оси мира и проходит через центр сферы, называется небесным экватором.
Большой круг PNnPsZ называется меридианом наблюдателя. Ось мира делит его на полуденную PNzPs и полуночную PNnPsчасти.
Большие круги PNCPs , плоскости которых проходят через полюсы мира, называют небесными меридианами, или кругами склонений. Большие круги гСп, плоскости которых проходят через отвесную линию (точки зенита и надира), называют вертикалами, или кругами высоты. Вертикал, проходящий через точки Е и W, называется первым вертикалом.
Малые кругиPСР', плоскости которых параллельны плоскости небесного экватора, называются небесными параллелями. Малые круги аСа', плоскости которых параллельны плоскости истинного горизонта, называются альмукантаратами.
Плоскость экватора наклонна к плоскости горизонта под углом 90° - f. Ось мира составляет с плоскостью истинного горизонта угол, равный географической широте f места наблюдателя.
